|
|
Dạng I: Tính xác suất của một biến cố theo định nghĩa cổ điển
Cách giải: Để tính xác suất $P(A)$ của một biến cố $A$ ta thực hiện các bước
+ Xác định không gian mẫu $\Omega$, rồi tính số phần tử $n(\Omega)$ của $\Omega.$
+ Xác định tập con mô tả biến cố $A,$ rồi tính số phần tử $n(A)$ của tập hợp $A$.
+ Tính $P(A)$ theo công thức $P(A)=\displaystyle \frac{n(A)}{n(\Omega)}$.
Thí dụ $1$. Một tổ học sinh gồm $9$ em, trong đó có $3$ nữ được chia thành $3$ nhóm đều nhau. Tính xác suất để mỗi nhóm có $1$ nữ.
Lời giải. Gọi $A$ là biến cố : “ ở $3$ nhóm học sinh mỗi nhóm có $1$ nữ”.
+ Để tìm $n(\Omega)$ ta thực hiện
Chọn ngẫu nhiên $3$ trong $9$ em đưa vào nhóm thứ nhất, số khả năng là $C_9^3$.
Chọn $3$ trong số $6$ em còn lại đưa vào nhóm thứ hai, số khả năng là $C_6^3.$
Chọn $3$ em đưa vào nhóm thứ $3,$ số khả năng là $C_3^3=1.$
Vậy $n(\Omega) = C_9^3. C_6^3. 1=1680$.
Vì phân ngẫu nhiên nên các biến số sơ cấp trong không gian biến cố sơ cấp này có cùng khả năng xuất hiện.
Để tìm $n(A)$ ta thực hiện
Phân $3$ nữ vào $3$ nhóm nên có $3!$ Cách khác nhau.
Phân $6$ nam vào $3$ nhóm theo cách như trên, ta có $C_6^2. C_4^2. 1$ cách khác nhau
Suy ra $n(A) = 3!.C_9^3. C_6^3. 1=540$.
+ Do đó $P(A)=\displaystyle \frac{n(A)}{n(\Omega)}=\displaystyle \frac{540}{1680}=\frac{27}{84}$
DẠNG II. Tính xác suất bằng quy tắc cộng
Cách giải. Sử dụng kỹ thuật đếm và các công thức sau để tính xác suất của biến cố đối, biến cố hợp,
$P(\overline{A})=1-P(A); P(A \cup B)=P(A)+P(B)$, nếu $A \cap B= \emptyset$.
Thí dụ $2$: Một hộp đựng $8$ viên bi xanh và $4$ viên bi đỏ. Lấy ngẫu nhiên $3$ viên bi. Tính xác suất để
a) Lấy được $3$ viên bi cùng màu.
b) Lấy được $3$ viên bi khác màu.
c) Lấy được ít nhất $2$ viên bi xanh.
Lời giải:
a) gọi $A$ là biến cố “ Lấy được $3$ viên bi xanh”, $B$ là biến cố “ lấy được $3$ viên bi đỏ” và $H $ là biến cố “ lấy được $3$ viên bi cùng màu”. Ta có $H=A \cup B$, vì $A$ và $B$ xung khắc nên $P(H) = P(A) + P(B)$.
Ta có $P(A)=\frac{C_8^3}{C_{12}^3}=\frac{14}{55}; P(B)=\frac{C_4^3}{C_{12}^3}=\frac{1}{55}$.
Từ đó $P(H)=\frac{14}{55}+\frac{1}{55}=\frac{3}{11}$.
b) Biến cố “ lấy được $3$ viên bi khác màu” là biến cố $\overline{H}$, Vậy
$P(\overline{H})=1-P(H)=1-\frac{3}{11}=\frac{8}{11}$
c) Gọi $C$ là biến cố lấy được $2$ viên bi xanh và một viên bi đỏ” , K là biến cố “ lấy được ít nhất $2$ viên bi xanh”. Ta có $K=A \cup C$ , vì $A$ và $C$ xung khắc, nên $P(K) = P(A) + P(C)$
Ta có $P(C)=\frac{C_8^2.C_4^1}{C_{12}^3}=\frac{28}{55}$
Suy ra $P(K)=\frac{14}{55}+\frac{28}{55}=\frac{42}{55}$
DẠNG III. Tính xác suất bằng quy tắc nhân
Cách giải. Để tính xác suất của biến cố giao của hai biến cố độc lập $A$ và $B$ ta dùng công thức $P(AB) =P(A)P(B)$
Thí dụ $3$. Có hai hộp chứa các quả cầu. Hộp thứ thất chứa $3$ quả cầu trắng, $7$ quả cầu đỏ và $15$ quả cầu xanh. Hộp thứ hai chứa $10$ quả cầu trắng, $6$ quả cầu đỏ và $9$ quả cầu xanh. Từ mỗi hộp lấy ngẫu nhiên ra một quả cầu . Tính xác suất để hai quả cầu lấy ra có màu giống nhau.
Lời giải : Gọi $A$ là biến cố "Quả cầu được lấy ra từ hộp thứ nhất là màu trắng", $B$ là biến cố "Quả cầu được lấy ra từ hộp thứ hai là màu trắng".
Ta có $P(A)=\frac{3}{25}, P(B)=\frac{10}{25}$. Vậy xác suất để hai quả cầu được lấy ra đều màu trắng là
$P(AB) = P(A) P(B) =\frac{3}{25}.\frac{10}{25}=\frac{30}{625}$( do $A, B$ độc lập)
Tương tự, xác suất để hai quả cầu được lấy ra đều màu xanh là $\frac{15}{25}.\frac{9}{25}=\frac{135}{625}$, và xác suất để lấy ra hai quả cầu đều màu đỏ là $\frac{6}{25}.\frac{7}{25}=\frac{42}{625}.$
Theo quy tắc cộng, xác suất để lấy ra hai quả cầu cùng màu là
$\frac{30}{625}+\frac{135}{625}+\frac{42}{625}=\frac{207}{625}$.
Dạng IV. Lập bảng phân bố xác suất của biến ngẫu
nhiên rời rạc.
Cách giải : Để lập bảng phân bố xác suất của biến ngẫu nhiên rời rạc $X$ ta thực
hiện các bước :
+ Xác định tập các giá trị có thể $\left\{ {x_1,x_2,\cdots,x_n} \right\}$ của $X$.
+ Tính các xác suất $p_i=P(X=x_i),$ trong đó $\left\{ {X=x_i} \right\}$ là biến
cố "$X$ nhận giá trị $x_i$".
+ Trình bày bảng phân bố xác suất theo dạng sau
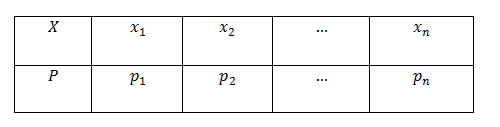
Ví dụ $4.$ Một lô hàng gồm $10$ sản phẩm trong đó có $3$ sản phẩm xấu. Chọn ngẫu
nhiên cùng lúc $4$ sản phẩn để kiểm tra. Gọi $X$ là số sản phẩm xấu gặp phải
khi kiểm tra. Lập bảng phân bố xác suất của $X$.
Lời giải :
Dễ thấy $X$ nhận các giá trị thuộc tập $\left\{ {0,1,2,3} \right\}$. Ta có :
$P(X=0)=\frac{C_7^4}{C_{10}^4}=\frac{35}{210}$
$P(X=1)=\frac{C_3^1.C_7^3}{C_{10}^4}=\frac{105}{210}$
$P(X=2)=\frac{C_3^2.C_7^2}{C_{10}^4}=\frac{63}{210}$
$P(X=3)=\frac{C_3^3.C_7^1}{C_{10}^4}=\frac{7}{210}$
Vậy bảng phân bố xác suất của $X$ là
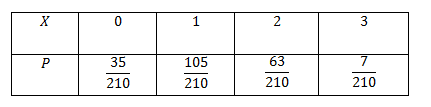
Dạng V. Tính kỳ vọng, phương sai, độ lệch chuẩn của biến ngẫu nhiên rời rạc.
Cách giải : Để tính kỳ vọng, phương sai và độ lệch chuẩn của biến ngẫu nhiên rời
rạc $X$ ta dùng các công thức :
$E(X)=\sum_{i=1}^{n}x_ip_i; V(X)=\sum_{i=1}^{n}(x_i-\mu)^2p_i$ hoặc
$V(X)=\sum_{i=1}^{n}x_i^2p_i-\mu^2; \sigma(X)=\sqrt{V(X)}$, trong đó
$p_i=P(X=x_i), \forall i=\overline{1,n}; \mu=E(X)$.
Ví dụ $5$. Một chiếc hộp đựng $10$ tấm thẻ, trong đó có bốn thẻ ghi số $1$, ba
thẻ ghi số $2$, hai thẻ ghi số $3$ và một thẻ ghi số $4$. Chọn ngẫu nhiên hai tấm
thẻ rồi cộng hai số trên hai tấm thẻ với nhau. Gọi $X$ là số thu được.
a) Lập bảng phân bố xác suất của $X$.
b) Tính kì vọng, phương sai và độ lệch chuẩn của $X$.
Lời giải :
a) Gọi $A_{ij}$ là biến cố "Chọn được tấm thẻ ghi số $i$ và tấm thẻ ghi số
$j$."
Dễ thấy $X$ nhận các giá trị thuộc tập $\left\{ {2,3,4,5,6,7} \right\}$. Ta có
:
$P(X=2)=P(A_{11})=\frac{C_4^2}{C_{10}^2}=\frac{6}{45}$
$P(X=3)=P(A_{12})=\frac{C_4^1.C_3^1}{C_{10}^2}=\frac{12}{45}$
$P(X=4)=P(A_{13})+P(A_{22})=\frac{C_4^1.C_2^1}{C_{10}^2}+\frac{C_3^2}{C_{10}^2}=\frac{11}{45}$
$P(X=5)=P(A_{14})+P(A_{23})=\frac{C_4^1.C_1^1}{C_{10}^2}+\frac{C_3^1.C_2^1}{C_{10}^2}=\frac{10}{45}$
$P(X=6)=P(A_{33})+P(A_{24})=\frac{C_2^2}{C_{10}^2}+\frac{C_3^1.C_1^1}{C_{10}^2}=\frac{4}{45}$
$P(X=7)=P(A_{34})=\frac{C_2^1.C_1^1}{C_{10}^2}=\frac{2}{45}$
Vậy bảng phân bố xác suất của $X$ là

b) Ta có :
$E(X)=2.\frac{6}{45}+3.\frac{12}{45}+4.\frac{11}{45}+5.\frac{10}{45}+6.\frac{4}{45}+7.\frac{2}{45}=4$
$V(X)=2^2.\frac{6}{45}+3^2.\frac{12}{45}+4^2.\frac{11}{45}+5^2.\frac{10}{45}+6^2.\frac{4}{45}+7^2.\frac{2}{45}-4^2
\approx 1,78.$
$\sigma(X)=\sqrt{V(X)}=\sqrt{1,78}\approx 1,33.$
BÀI TẬP ÁP DỤNG
$1$. Một hộp đựng $12$ quả cầu cùng kích thước trong đó có $3$ quả cầu xanh, $4$ quả cầu đen và $5$ quả cầu trắng. Chọn nhẫu nhiên cùng lúc $4$ quả cầu. tính xác suất để trong $4$ quả cầu chọn được có
a) $4$ quả cầu cùng màu.
b) $2$ quả cầu trắng.
c) $1$ quả cầu trắng, $1$ quả cầu đen.
$2$. Gieo đồng thời đồng $5$ xu. Tính xác suất để
a) được $3$ mặt ngửa.
b) có ít nhất $3$ mặt ngửa.
c) có ít nhất $1$ mặt ngửa.
$3$. Hai bạn Đào và Mai học xa nhà. Xác suất để Đào và Mai về thăm nhà vào ngày chủ nhật tương ứng là $0,2$ và $0,25$. Tính xác suất để vào ngày chủ nhật
a) cả hai về thăm nhà.
b) cả hai không về thăm nhà.
c) có đúng $1$ người về thăm nhà.
d) có ít nhất $1$ người về thăm nhà.
$4.$ Một hộp đề thi vấn đáp có $30$ câu hỏi, trong đó có $10$
câu hỏi khó. Một học sinh cần rút
ngẫu nhiên $3$ câu hỏi để trả lời. Gọi $X$ là số câu khó trong số $3$ câu hỏi
đã rút ra.
a) Lập bảng phân bố xác suất của $X$.
b) Tính xác suất để học sinh này chỉ nhận được toàn câu khó.
c) Tính xác suất để học sinh này nhận được ít nhất $2$ câu khó.
d) Tính kỳ vọng, phương sai và độ lệch chuẩn của $X$.
|