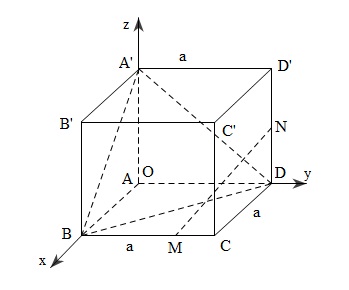
a) Chọn hệ trục tọa độ $Oxyz$ như sau:
Gốc $O\equiv A$
Trục $Ox$ đi qua $AB$
Trục $Oy$ đi qua $AD$
Trục $Oz$ đi qua $AA'$
Khi đó $A(0;0;0), B(a;0;0), D(0;a;0), A'(0;0;a)$
Phương trình mặt phẳng $(A'BD)$ có dạng:
$\frac{x}{a}+\frac{y}{a}+\frac{z}{a}=1\Leftrightarrow x+y+z-a=0 $
Vecto pháp tuyến của $A'BD:\overrightarrow{n}:(1;1;1) $
$M$ là trung điểm của $BC\Rightarrow M(a;\frac{a}{2};0 )$
$N$ là trung điểm của $DD'\Rightarrow N(0;a;\frac{a}{2} )$
$\Rightarrow \overrightarrow{MN}=(-a;\frac{a}{2};\frac{a}{2} ) \Rightarrow \overrightarrow{n}.\overrightarrow{MN} =-a+\frac{a}{2}+\frac{a}{2}=0\Rightarrow \overrightarrow{n}\bot \overrightarrow{MN} $
vậy $MN//(A'BD)$
b) Ta có: $MN//(A'BD)$ chứa $BD$
$\Rightarrow $ khoảng cách giữa $MN$ và $BD$ là khoảng cách từ $M$ đến mặt phẳng $(A'BD)$
$\Rightarrow d(MN,BD)=d(M,(A'BD))=\frac{|a+\frac{a}{2}-a |}{\sqrt{3} }=\frac{a}{2\sqrt{3} } =\frac{a\sqrt{3} }{6} $